
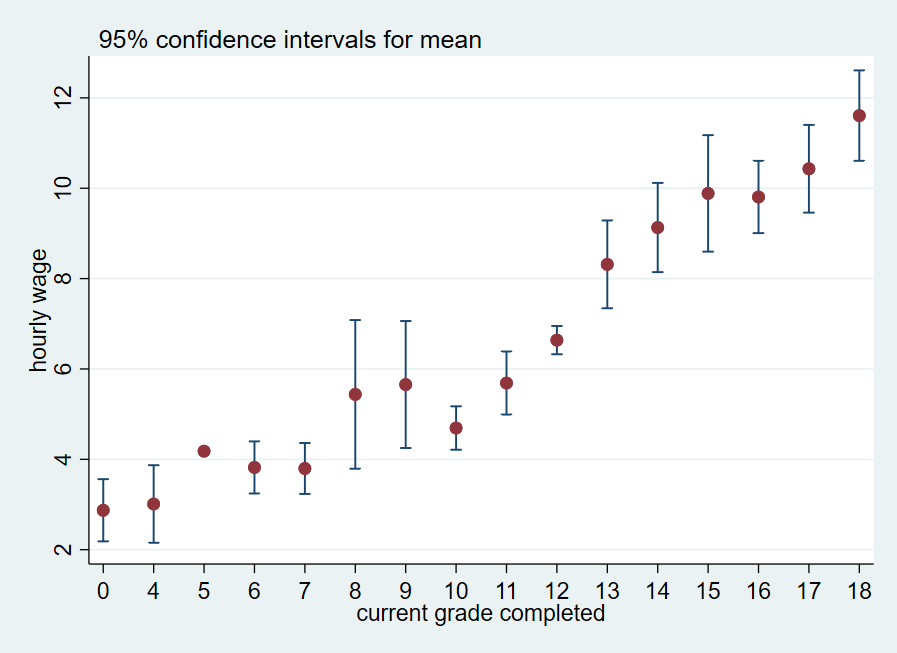
This model is a mathematical representation of data variability, and thus ideally would capture accurately all sources of such variability.
STATA CONFIDENCE INTERVAL FULL
The full set of assumptions is embodied in a statistical model that underpins the method. Statistical models, hypotheses, and testsĮvery method of statistical inference depends on a complex web of assumptions about how data were collected and analyzed, and how the analysis results were selected for presentation.

Specific issues are covered at length in these sources and in the many peer-reviewed articles that critique common misinterpretations of null-hypothesis testing and “statistical significance”. More detailed discussion of the general issues can be found in many articles, chapters, and books on statistical methods and their interpretation. Among the many reasons are that, in most scientific settings, the arbitrary classification of results into “significant” and “non-significant” is unnecessary for and often damaging to valid interpretation of data and that estimation of the size of effects and the uncertainty surrounding our estimates will be far more important for scientific inference and sound judgment than any such classification. We further explain why statistical tests should never constitute the sole input to inferences or decisions about associations or effects. We also discuss a few more subtle but nonetheless pervasive problems, explaining why it is important to examine and synthesize all results relating to a scientific question, rather than focus on individual findings. Toward that end, we attempt to explain the meaning of significance tests, confidence intervals, and statistical power in a more general and critical way than is traditionally done, and then review 25 common misconceptions in light of our explanations. We thus think it imperative that basic teaching as well as general understanding of these methods be improved. ĭespite such bans, we expect that the statistical methods at issue will be with us for many years to come. One journal now bans all statistical tests and mathematically related procedures such as confidence intervals, which has led to considerable discussion and debate about the merits of such bans. Misinterpretation and abuse of statistical tests has been decried for decades, yet remains so rampant that some scientific journals discourage use of “statistical significance” (classifying results as “significant” or not based on a P value). We conclude with guidelines for improving statistical interpretation and reporting. We then provide an explanatory list of 25 misinterpretations of P values, confidence intervals, and power.
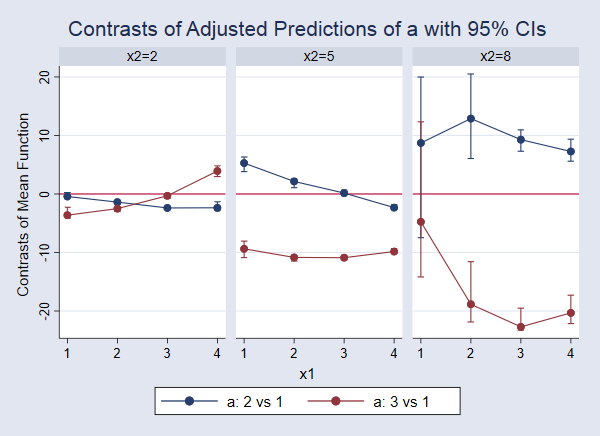
We emphasize how violation of often unstated analysis protocols (such as selecting analyses for presentation based on the P values they produce) can lead to small P values even if the declared test hypothesis is correct, and can lead to large P values even if that hypothesis is incorrect. Our goal is to provide a resource for instructors, researchers, and consumers of statistics whose knowledge of statistical theory and technique may be limited but who wish to avoid and spot misinterpretations. In light of this problem, we provide definitions and a discussion of basic statistics that are more general and critical than typically found in traditional introductory expositions. This high cognitive demand has led to an epidemic of shortcut definitions and interpretations that are simply wrong, sometimes disastrously so-and yet these misinterpretations dominate much of the scientific literature. Instead, correct use and interpretation of these statistics requires an attention to detail which seems to tax the patience of working scientists. A key problem is that there are no interpretations of these concepts that are at once simple, intuitive, correct, and foolproof. Misinterpretation and abuse of statistical tests, confidence intervals, and statistical power have been decried for decades, yet remain rampant.


 0 kommentar(er)
0 kommentar(er)
